Tính hóa học trực tâm của tam giác - Những điều thú vị bạn phải nhà lao phá
Chủ đề Tính hóa học trực tâm của tam giác: Tam giác đem đặc thù trực tâm vô nằm trong quan trọng và thú vị. Trực tâm là vấn đề uỷ thác của tía đàng cao nhập tam giác, tạo ra trở nên một góc vuông. Nó cũng chính là uỷ thác điểm của tía đàng trung tuyến, là điểm triệu tập sự tương tác và cân đối Một trong những thành phần của tam giác. Tính hóa học này gom tất cả chúng ta tò mò và làm rõ rộng lớn về cấu tạo và hình dạng tam giác, đưa đến sự thú vị và thưởng thức tiếp thu kiến thức ấn tượng.
Bạn đang xem: trực tâm là gì
Tính hóa học trực tâm của tam giác là vấn đề uỷ thác của tía đàng cao. Mỗi tam giác đem đích thị tía đàng cao, đàng cao kể từ từng đỉnh của tam giác cho tới đối lập của chính nó. Điểm uỷ thác này được gọi là trực tâm.
Đặc điểm cần thiết của trực tâm là những đường thẳng liền mạch kể từ trực tâm cho tới những đỉnh của tam giác tạo ra trở nên những góc vuông với những cạnh ứng. Vì vậy, trực tâm là điểm triệu tập của những đàng cao và cũng là vấn đề trọng tâm của tam giác.
Ngoài đi ra, trực tâm còn là vấn đề uỷ thác của tía đàng trung tuyến. Đường trung tuyến nhập tam giác là đoạn trực tiếp nối trung điểm của nhị đỉnh của tam giác với trung điểm của cạnh chứa chấp đỉnh loại tía.
Tính hóa học trực tâm của tam giác đặc biệt hữu dụng trong các việc giải những vấn đề tam giác, nhất là trong các việc thăm dò trọng tâm và những thông số kỹ thuật tương quan không giống của tam giác.

Tam giác đem từng nào trực tâm?
Tam giác đem độc nhất một trực tâm. Trực tâm của tam giác là vấn đề uỷ thác của tía đàng cao. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác với đường thẳng liền mạch trải qua đỉnh đối lập. Trực tâm cũng chính là uỷ thác điểm của tía đàng trung tuyến nhập tam giác. Đường trung tuyến của một cạnh nhập tam giác là đoạn trực tiếp nối trung điểm của cạnh ê với đỉnh đối lập.
Đặc điểm của những đàng cao nhập tam giác?
Các đàng cao nhập tam giác đem những Điểm sáng sau:
1. Đường cao từ là một đỉnh của tam giác là đoạn trực tiếp nối đỉnh ê với đối lập của chính nó.
2. Ba đàng cao của tam giác uỷ thác nhau bên trên một điểm độc nhất, gọi là trực tâm.
3. Trực tâm là uỷ thác điểm của tía đàng cao, nghĩa là vấn đề tuy nhiên kể từ ê kẻ đàng cao cho tới từng đỉnh của tam giác đều tạo ra trở nên một góc vuông.
4. Trực tâm ở trong tam giác nếu như tam giác ko nên là tam giác vuông.
5. Nếu tam giác là tam giác vuông, trực tâm phía trên đỉnh thành phần của đỉnh góc vuông.
6. Trực tâm là trọng tâm của tam giác đều.
7. Hai đàng cao còn sót lại hạn chế nhau và với đàng cao từ là một đỉnh tạo ra trở nên tía góc vuông.
8. Đường cao của một tam giác cũng đó là đàng phân giác của góc đối lập với đỉnh nằm trong đàng cao ê.
Tóm lại, những đàng cao của tam giác nối liền với không hề ít Điểm sáng cần thiết nhập tam giác, nhất là trực tâm và những góc vuông.
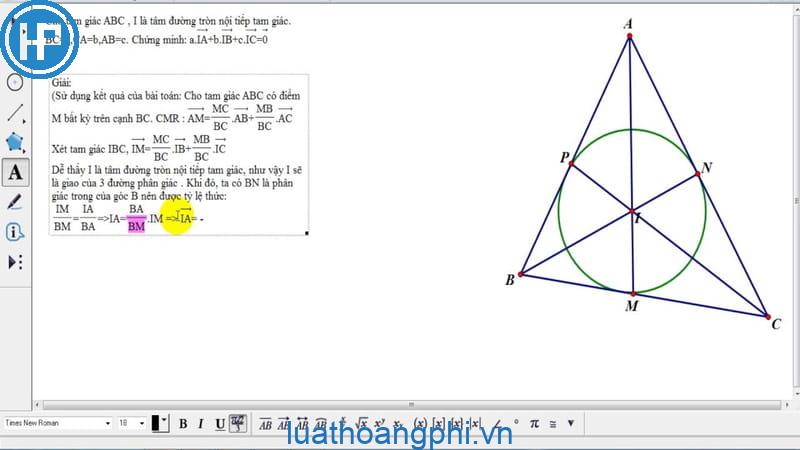
Trực Tâm Tam Giác - Tính Chất Đặc Biệt và Cách Xác Định
Tính hóa học trực tâm: Khám đập phá bí ẩn của đặc thù trực tâm nhập hình học! Video tiếp tục khiến cho bạn làm rõ về tâm của một tam giác và những Điểm sáng rất dị tuy nhiên đặc thù trực tâm đưa đến. Đón coi ngay lập tức nhằm tò mò thêm thắt về điều thú vị này!
Đường trung tuyến đem nút giao công cộng nào là nhập tam giác?
Trong một tam giác, đàng trung tuyến đem nút giao công cộng bên trên trực tâm của tam giác. Đường trung tuyến của một cạnh nhập tam giác là đường thẳng liền mạch nối trung điểm của cạnh ê với đỉnh đối lập. Vì vậy, tam giác đem tía đàng trung tuyến, và đều hạn chế nhau bên trên một điểm công cộng là trực tâm.
Trực tâm là gì?
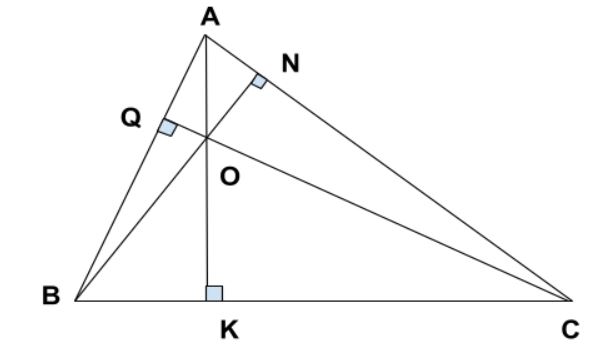
Trực tâm của một tam giác là vấn đề uỷ thác của tía đàng cao nhập tam giác ê. Đường cao nhập tam giác là đoạn trực tiếp nối một đỉnh của tam giác với đối lập của chính nó và trải qua trọng tâm của tam giác. Trong một tam giác ngẫu nhiên, tớ rất có thể thăm dò trực tâm bằng phương pháp uỷ thác nhau của tía đàng cao, tức là thăm dò điểm tuy nhiên đàng cao kể từ từng đỉnh của tam giác đều uỷ thác nhau. Trực tâm rất có thể được xem như là trọng tâm của tam giác, vì như thế nó là vấn đề khoảng của những điểm đỉnh của tam giác.
Xem thêm: Trang web Ve Bo TV - Tận hưởng các trận đấu hấp dẫn nhất
_HOOK_
Trực Tâm Tam Giác - Tính Chất và Ứng Dụng - Toán Lớp 7
Ứng dụng - Toán lớp 7: quý khách hàng đang được quan hoài cho tới phần mềm của toán học? Video về phần mềm toán lớp 7 tiếp tục đưa về cho mình những ví dụ thực tiễn nhằm vận dụng kỹ năng toán nhập cuộc sống mỗi ngày. Mở rộng lớn tầm đôi mắt trải qua video clip này và thăm dò hiểu thêm thắt về sự việc hữu ích của toán học!
Trong một tam giác, đem từng nào đàng trung tuyến?
Trong một tam giác, đem tía đàng trung tuyến. Đường trung tuyến của một tam giác là đoạn trực tiếp nối trung điểm của những cạnh của tam giác. Vậy nên, nhập một tam giác, đem tía đàng trung tuyến, từng đàng trung tuyến nối trung điểm của nhị cạnh của tam giác.
Đường trung tuyến là đoạn ở Một trong những điểm nào?
Đường trung tuyến là đoạn trực tiếp nối trung điểm của nhị đỉnh của tam giác với trực tâm của tam giác.

Điểm uỷ thác của tía đàng cao nhập tam giác là gì?
Điểm uỷ thác của tía đàng cao nhập tam giác được gọi là trực tâm.
Ba đàng cao là những đường thẳng liền mạch lên đường kể từ từng đỉnh của tam giác cho tới đối lập của chính nó sao mang đến tạo ra trở nên một góc vuông.
Để thăm dò trực tâm, tớ rất có thể tuân theo quá trình sau:
1. Vẽ tam giác và xác lập những đỉnh của tam giác.
2. Vẽ 3 đường thẳng liền mạch cao kể từ từng đỉnh của tam giác cho tới đối lập của chính nó. Đây là những đường thẳng liền mạch trải qua đỉnh và vuông góc với cạnh đối lập.
3. Tìm uỷ thác điểm của tía đàng cao, nút giao này đó là trực tâm của tam giác.
4. Đánh vệt và ghi lưu giữ địa điểm của trực tâm nhập tam giác.
Chúng tớ rất có thể dùng những công thức và đặc thù của tam giác nhằm tính những địa điểm và tọa phỏng của đỉnh tam giác, cạnh và góc nhập tam giác. Tuy nhiên, nhằm đáp ứng tính đúng chuẩn, tương đối đầy đủ và hiệu suất cao, tớ nên dùng dụng cụ tương hỗ đo lường hoặc ứng dụng hình đồ họa nhằm vẽ và đo lường tam giác và nút giao của tía đàng cao.
Đường Trung Tuyến, Đường Trung Trực, Đường Cao, Đường Phân Giác nhập Tam Giác
Đường trung tuyến, đàng trung trực, đàng cao, đàng phân giác: Muốn làm rõ về những loại đàng quan trọng nhập tam giác? Video này tiếp tục trả lời toàn cỗ vướng mắc của người tiêu dùng về đàng trung tuyến, đàng trung trực, đàng cao và đàng phân giác. Cùng tò mò những Điểm sáng rất dị và phần mềm thú vị của bọn chúng qua chuyện video clip này!
Tam giác cần thiết thoả mãn ĐK gì để sở hữu được trực tâm?
Để một tam giác đạt được trực tâm, những ĐK sau rất cần được thoả mãn:
1. Điều khiếu nại cần: Tam giác nên là tam giác không được đều với tía cạnh ko đều bằng nhau và những góc ko đều bằng nhau. Nếu tam giác là tam giác cân nặng, cạnh đối xứng hoặc tam giác đều, tức là đem những cạnh và góc tương tự, thì tam giác không tồn tại trực tâm.
2. Điều khiếu nại đủ: Tam giác nên đem tía đàng cao và tía đàng trung tuyến.
- Đường cao nhập tam giác là đường thẳng liền mạch liên kết một đỉnh của tam giác với đối lập của chính nó, và trải qua trực tâm.
- Đường trung tuyến nhập tam giác là đoạn trực tiếp nối trung điểm của những cạnh cùng nhau. Ba đàng trung tuyến của tam giác nên hạn chế nhau bên trên một điểm độc nhất, tức là trực tâm.
Tóm lại, nhằm tam giác đạt được trực tâm, tam giác nên không được đều và nên đem tía đàng cao và tía đàng trung tuyến, nhập ê tía đàng cao hạn chế nhau bên trên một điểm độc nhất, được gọi là trực tâm.
Xem thêm: phim trung quốc mới nhất
Đường cao là đoạn trực tiếp nối điểm nào là nhập tam giác?
Đường cao là đoạn trực tiếp nối một đỉnh của tam giác với điểm trung điểm của cạnh đối lập nó.
_HOOK_
Sử Dụng Tính Chất Trực Tâm nhằm Chứng Minh Đồng Quy - Toán 7 - Cô Hạnh (Dễ Hiểu Nhất)
Chứng minh đồng quy - Toán 7 - Cô Hạnh: Học cơ hội minh chứng đồng quy nhập môn toán lớp 7 với cô Hạnh. Video này tiếp tục khiến cho bạn làm rõ về cách thức minh chứng này trải qua những ví dụ minh họa và quá trình rõ ràng. Hãy nằm trong nhập cuộc và nâng lên kĩ năng toán học tập của tớ với cô Hạnh!





Bình luận