Chủ đề Công thức tính chừng nhiều năm đàng chéo cánh hình thoi: Công thức tính chừng nhiều năm đàng chéo cánh hình thoi là 1 trong những công thức giản dị và đơn giản và dễ nắm bắt. Nếu biết chừng nhiều năm cạnh của hình thoi, tớ chỉ việc vận dụng công thức nhằm tính chừng nhiều năm đàng chéo cánh. Ví dụ, nếu như chừng nhiều năm cạnh của hình thoi là 5, tớ rất có thể tính đàng chéo cánh bằng phương pháp vận dụng công thức căn bậc nhị của (5)² + (5)². Việc đo lường và tính toán này canh ty tất cả chúng ta hiểu thêm thắt về hình thoi và thao tác với nó một cơ hội đơn giản và hiệu suất cao.
Cách tính chừng nhiều năm đàng chéo cánh hình thoi là gì?
Cách tính chừng nhiều năm đàng chéo cánh của hình thoi là dùng công thức AC = BD = a, nhập ê a là chừng nhiều năm cạnh của hình thoi. Đây là công thức giản dị và đơn giản và dễ nắm bắt. Ví dụ, nếu như hình thoi có tính nhiều năm cạnh là 5, thì chừng nhiều năm đàng chéo cánh của hình thoi được xem là căn bậc nhị của (5)² + (5)², tương tự với căn bậc nhị của 50, thành phẩm là 7.07.
Bạn đang xem: tính đường chéo hình thoi
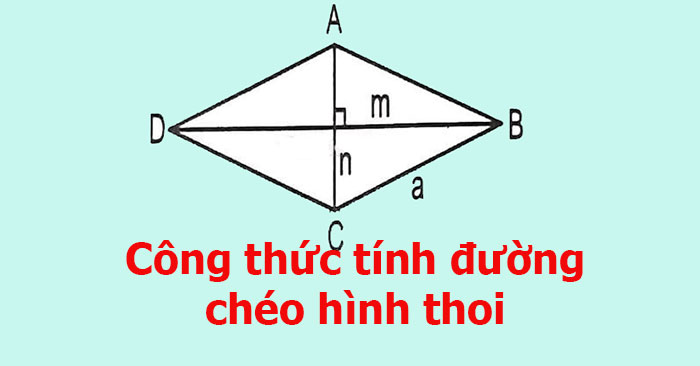
Công thức tính chừng nhiều năm đàng chéo cánh hình thoi là gì?
Công thức tính chừng nhiều năm đàng chéo cánh của hình thoi là AC = BD = a, nhập ê a là chừng nhiều năm cạnh của hình thoi. Đây là 1 trong những trong mỗi công thức giản dị và đơn giản và dễ nắm bắt nhất nhằm tính chừng nhiều năm đàng chéo cánh của hình thoi.
Độ nhiều năm đàng chéo cánh hình thoi được xem như vậy nào?
Độ nhiều năm đàng chéo cánh hình thoi được xem vì thế công thức sau: \"Đường chéo cánh vì thế căn bậc nhị của tổng bình phương chừng nhiều năm cạnh\".
Cụ thể, nếu như tớ với hình thoi ABCD có tính nhiều năm cạnh là a, thì chừng nhiều năm đàng chéo cánh của hình thoi tiếp tục là: AC = BD = căn bậc nhị của (a)² + (a)².
Ví dụ, nếu như hình thoi có tính nhiều năm cạnh là 5, tớ tính chừng nhiều năm đàng chéo cánh như sau: Đường chéo cánh = căn bậc nhị của (5)² + (5)² = căn bậc nhị của 50 = 7.07 (đơn vị đo chừng dài).
Như vậy, nhằm tính chừng nhiều năm đàng chéo cánh hình thoi, tớ chỉ việc lấy tổng bình phương chừng nhiều năm cạnh, và tiếp sau đó lấy căn bậc nhị của thành phẩm ê.
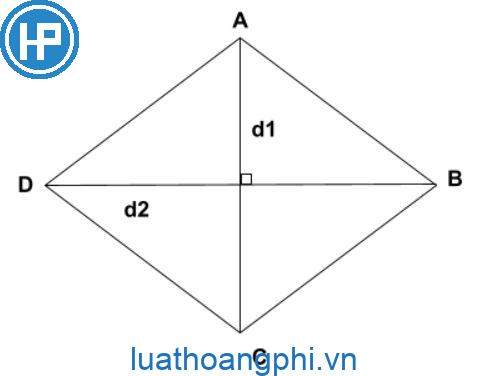
Làm sao nhằm tính chừng nhiều năm đàng chéo cánh hình thoi lúc biết độ quý hiếm cạnh?
Để tính chừng nhiều năm đàng chéo cánh của hình thoi lúc biết độ quý hiếm cạnh, tất cả chúng ta rất có thể dùng công thức sau: \"đường chéo cánh = căn bậc nhị của (độ nhiều năm cạnh)² + (độ nhiều năm cạnh)²\".
Ví dụ, nếu như hình thoi có tính nhiều năm cạnh là 5 thì tớ triển khai như sau:
Đường chéo cánh = căn bậc nhị của (5)² + (5)² = căn bậc nhị của 50 = 7.07 (đơn vị).
Vậy, chừng nhiều năm đàng chéo cánh của hình thoi khi cạnh có mức giá trị là 5 là 7.07.
Công thức này được dùng làm tính chừng nhiều năm đàng chéo cánh hình thoi một cơ hội giản dị và đơn giản và dễ nắm bắt.
Có cơ hội tính đường chéo hình thoi này dễ nắm bắt và giản dị và đơn giản không?
Có một cơ hội tính đường chéo hình thoi dễ nắm bắt và giản dị và đơn giản như sau:
1. Gọi cạnh hình thoi là a.
2. Sử dụng công thức Pythagoras nhằm tính đàng chéo cánh.
3. Theo công thức Pythagoras, đàng chéo cánh bình phương vì thế tổng bình phương nhị cạnh.
4. Vì hình thoi với nhị cạnh cân nhau, nên tớ dành được công thức đàng chéo cánh là căn bậc nhị của (a)² + (a)².
5. Đơn giản hóa công thức, tớ với căn bậc nhị của 2(a)².
6. Kết trái ngược là đàng chéo cánh vì thế căn bậc nhị của 2 nhân với bình phương cạnh hình thoi.
Ví dụ: Nếu hình thoi với cạnh vì thế 5, tớ vận dụng công thức vẫn nêu trên:
Đường chéo cánh = căn bậc nhị của 2(5)² = căn bậc nhị của 50 = 7.07.
Vậy đấy là một cơ hội tính đường chéo hình thoi dễ nắm bắt và giản dị và đơn giản.
_HOOK_
Xem thêm: phim hài châu tinh trì
Cách tính chừng nhiều năm đàng chéo cánh hình thoi kể từ diện tích S và đàng chéo cánh hình thoi
Trong video clip này, tất cả chúng ta tiếp tục dò la hiểu về kiểu cách tính chừng nhiều năm đàng chéo cánh của hình thoi một cơ hội giản dị và đơn giản và dễ nắm bắt. Với những khêu gợi ý và bước giải cụ thể, các bạn sẽ đơn giản vận dụng kỹ năng và kiến thức này nhập những Việc hình học tập không giống.
Tính chừng nhiều năm đàng chéo cánh hình thoi kể từ diện tích S và đàng chéo cánh Toán lớp 4 5
Bạn ham muốn tính chừng nhiều năm đàng chéo cánh của hình thoi nhưng mà ko biết nên chính thức kể từ đâu? Đừng băn khoăn, video clip này tiếp tục chỉ cho chính mình phương pháp tính chừng nhiều năm đàng chéo cánh một cơ hội cụ thể và nhanh gọn. Hãy nằm trong coi và nắm rõ công thức nhằm xử lý từng Việc tương quan cho tới hình thoi.
Hãy mang lại ví dụ về sự tính chừng nhiều năm đàng chéo cánh hình thoi lúc biết độ quý hiếm cạnh?
Để tính chừng nhiều năm đàng chéo cánh của hình thoi, tất cả chúng ta rất có thể dùng công thức sau: Đường chéo cánh = căn bậc nhị của (cạnh)² + (cạnh)².
Ví dụ, fake sử tất cả chúng ta với 1 hình thoi có tính nhiều năm cạnh là 5. Để tính chừng nhiều năm đàng chéo cánh, tất cả chúng ta triển khai công việc sau:
1. sát dụng công thức: Đường chéo cánh = căn bậc nhị của (5)² + (5)².
2. Thực hiện tại phép tắc tính: Đường chéo cánh = căn bậc nhị của 25 + 25.
3. Tính tổng thân mật 25 và 25: Đường chéo cánh = căn bậc nhị của 50.
4. Tính căn bậc nhị của 50: Đường chéo cánh ≈ 7.07 (làm tròn trĩnh cho tới 2 chữ số thập phân).
Vì vậy, nếu như cạnh của hình thoi có tính nhiều năm là 5, thì chừng nhiều năm đàng chéo cánh được xem là khoảng chừng 7.07.
Nếu biết đàng chéo cánh hình thoi, làm thế nào nhằm dò la độ quý hiếm cạnh của hình thoi?
Nếu biết đàng chéo cánh của hình thoi, tớ rất có thể dò la độ quý hiếm cạnh của hình thoi bằng phương pháp dùng công thức tính chừng nhiều năm đàng chéo cánh hình thoi.
Công thức tính chừng nhiều năm đàng chéo cánh hình thoi là: AC = BD = a, nhập ê a là chừng nhiều năm cạnh của hình thoi.
Bước 1: Lấy độ quý hiếm của đàng chéo cánh hình thoi (AC hoặc BD).
Bước 2: Xác định vị trị cạnh của hình thoi bằng phương pháp thay cho thay đổi công thức bên trên.
Ví dụ:
Nếu đàng chéo cánh hình thoi có tính nhiều năm là 10 centimet, tớ dùng công thức AC = BD = a nhằm dò la độ quý hiếm cạnh của hình thoi.
AC = BD = a
10 centimet = a
Vậy, độ quý hiếm cạnh của hình thoi là 10 centimet.
Tại sao công thức tính đường chéo hình thoi với căn bậc nhị và công thức căn bậc nhị là như vậy nào?
Công thức tính chừng nhiều năm đàng chéo cánh của hình thoi bao gồm căn bậc nhị và công thức căn bậc nhị được dùng vì thế đặc thù của tam giác vuông.
1. Công thức tính đường chéo hình thoi là AC = BD = a, nhập ê a là chừng nhiều năm cạnh của hình thoi.
2. Để hiểu vì sao công thức tính đàng chéo cánh với căn bậc nhị, tớ dùng tam giác vuông với cạnh hình thoi là đàng chéo cánh. Theo ấn định lý Pythagoras, nhập một tam giác vuông, bình phương của cạnh huyền (h) vì thế tổng bình phương của nhị cạnh góc vuông (a, b). sát dụng lý thuyết này nhập tam giác vuông tạo ra trở thành vì thế đàng chéo cánh của hình thoi, tớ có:
- Hình thoi với cạnh là a, nên nhị cạnh góc vuông sẽ sở hữu được nằm trong chừng nhiều năm a/2.
- Đường chéo cánh của hình thoi là đàng chéo cánh của tam giác vuông này, nên cạnh huyền của tam giác vuông là chừng nhiều năm đàng chéo cánh của hình thoi. Ta ký hiệu chừng nhiều năm đàng chéo cánh là d.
- sát dụng công thức Pythagoras, tớ có: (d/2)^2 = (a/2)^2 + (a/2)^2 = 2(a/2)^2.
3. Để dò la chừng nhiều năm đàng chéo cánh d, tớ cần thiết tính căn bậc nhị của biểu thức 2(a/2)^2. Đây đó là nguyên vẹn nhân vì thế sao công thức tính đường chéo hình thoi chứa chấp căn bậc nhị.
4. Công thức căn bậc nhị nhằm tính độ quý hiếm của biểu thức bên trên là căn bậc nhị của a^2 = (a/2)^2 + (a/2)^2 = 2(a/2)^2. Để tính căn bậc nhị, tớ triển khai công việc sau:
- Ghi lại biểu thức cần thiết tính: 2(a/2)^2.
- Chia biểu thức mang lại 2: (a/2)^2.
- sát dụng căn bậc nhị nhập biểu thức vẫn chia: căn bậc nhị của (a/2)^2.
Với công việc bên trên, tớ rất có thể tính được chừng nhiều năm đàng chéo cánh của hình thoi bằng phương pháp dùng công thức tính đàng chéo cánh và công thức căn bậc nhị.
Xem thêm: kiến trúc thượng tầng
Có cơ hội tính đường chéo hình thoi không giống ko ngoài công thức căn bậc hai?
Có, ngoài công thức tính đường chéo hình thoi vì thế căn bậc nhị, còn tồn tại một cách thứ hai nhằm tính đường chéo hình thoi bằng phương pháp dùng ấn định lý Pythagoras. Định lý này cho rằng nhập một tam giác vuông, bình phương cạnh huyền (h) vì thế tổng bình phương nhị cạnh góc vuông (a và b). sát dụng ấn định lý Pythagoras nhập hình thoi, tớ có:
AC² = AB² + BC²
Vì AB và BC là nhị cạnh có tính nhiều năm cân nhau nhập hình thoi, tớ tiếp tục có:
AC² = a² + a² = 2a²
Do ê, chừng nhiều năm đàng chéo cánh hình thoi rất có thể tính vì thế căn bậc nhị của gấp đôi bình phương chừng nhiều năm cạnh:
AC = √(2a²)
Đây là cách thứ hai nhằm tính đường chéo hình thoi nhưng mà ko dùng công thức căn bậc nhị thẳng.
Làm sao nhằm tính diện tích S hình thoi lúc biết chừng nhiều năm đàng chéo?
Để tính diện tích S hình thoi lúc biết chừng nhiều năm đàng chéo cánh, tớ với 1 công thức giản dị và đơn giản như sau:
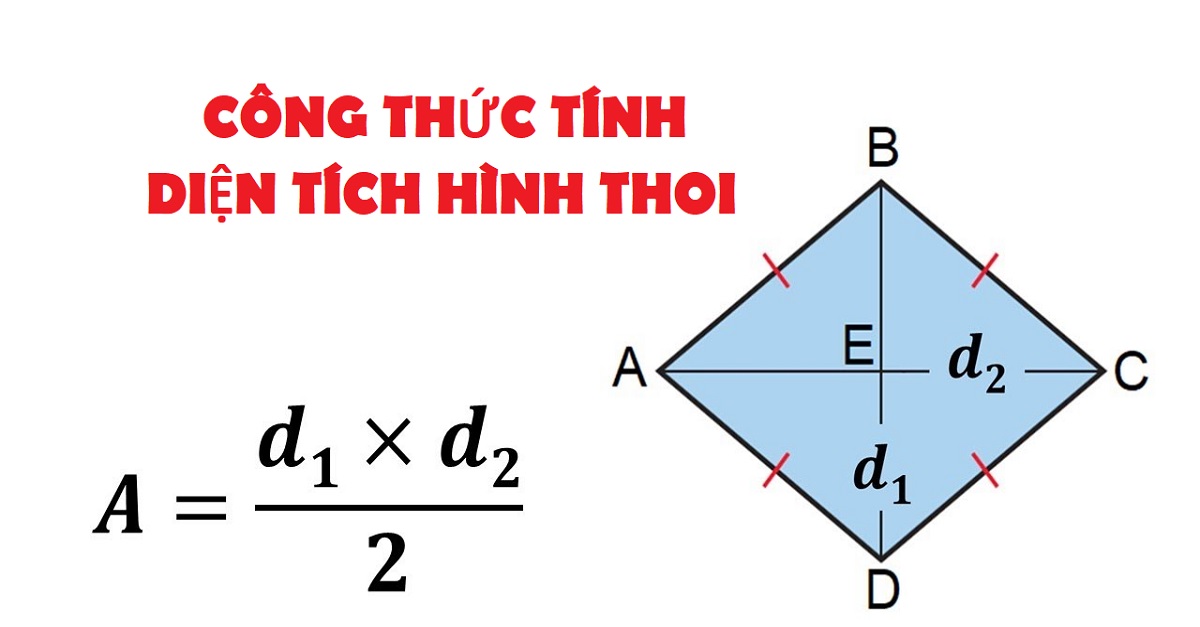
Diện tích hình thoi = (Đường chéo cánh chủ yếu * Đường chéo cánh phụ) / 2
Ví dụ, nếu khách hàng biết chừng nhiều năm đàng chéo cánh chủ yếu (AC) là 8 và đàng chéo cánh phụ (BD) là 6, chúng ta có thể tính diện tích S hình thoi như sau:
Diện tích hình thoi = (8 * 6) / 2 = 48 / 2 = 24
Vậy diện tích S hình thoi là 24 đơn vị chức năng vuông.
_HOOK_










Bình luận