Chủ đề chứng tỏ lối tầm của tam giác: Chứng minh lối tầm của tam giác là 1 trong những phép tắc chứng tỏ cần thiết vô hình học tập. Khi chứng tỏ lối tầm của tam giác, tớ hoàn toàn có thể vận dụng những quy tắc và đặc thù của đồng dạng, đồng quy, và đường thẳng liền mạch tuy vậy tuy vậy. Quá trình chứng tỏ này hỗ trợ chúng ta nắm rõ rộng lớn về cấu hình và đặc thù của tam giác, và giải quyết và xử lý những Việc tương quan cho tới lối tầm vô hình học tập.
Tìm công thức chứng tỏ lối tầm của tam giác?
Để chứng tỏ lối tầm của tam giác, tớ sở hữu công thức như sau:
Giả sử ABC là tam giác, và AD là lối tầm của cạnh BC.
Công thức nhằm chứng tỏ AD là lối tầm là:
1. Xác lăm le trung điểm M của cạnh BC.
2. Kẻ đường thẳng liền mạch AM.
3. Chứng minh AM phân chia cạnh BC trở nên nhị đoạn đều nhau, tức là BM = CM.
Để chứng tỏ, tớ hoàn toàn có thể dùng một vài cách thức như phép tắc chiếu, phép tắc đồng thay đổi, hoặc dùng những tính chất của tam giác. Tùy nằm trong vô Việc rõ ràng và công thức các bạn đang được học tập, bạn cũng có thể lựa lựa chọn cách thức thích hợp nhằm chứng tỏ.
Ví dụ: Cho tam giác ABC với trung điểm M của cạnh BC. Ta cần thiết chứng tỏ AM là lối tầm của cạnh BC.
Bước 1: Vẽ đường thẳng liền mạch AM.
Bước 2: Chứng minh rằng BM = CM.
Có thể chứng tỏ bằng phương pháp dùng đặc thù của trung tuyến, tức là đường thẳng liền mạch trải qua trung điểm của một cạnh tam giác tuy vậy song với cạnh loại tía.
Ở trên đây, tớ hoàn toàn có thể dùng đặc thù của trung tuyến nhằm chứng tỏ rằng BM = CM.
Bạn đang xem: cách chứng minh đường trung bình
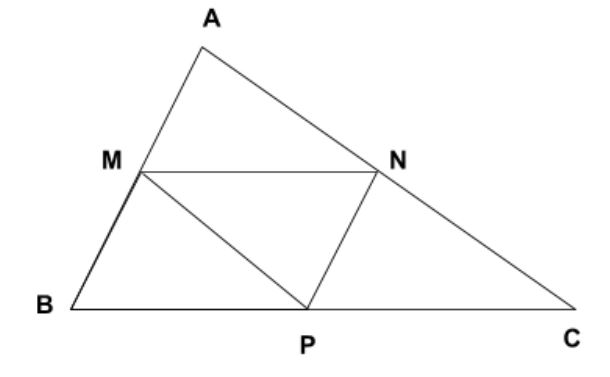

Định nghĩa lối tầm của tam giác là gì?
Đường tầm của tam giác là đoạn trực tiếp nối trung điểm của một cạnh với đỉnh đối lập. Nó là 1 trong những đường thẳng liền mạch trải qua trung điểm và tuy vậy song với cạnh đối lập. Đường tầm của tam giác tách đỉnh của tam giác vô một điểm độc nhất là trung điểm của cạnh sót lại.
Tại sao lối tầm của tam giác hoàn toàn có thể được xác lập là tuy vậy song với cạnh loại ba?
Để chứng tỏ rằng lối tầm của tam giác là tuy vậy song với cạnh loại tía, tớ hoàn toàn có thể dùng một vài cách thức chứng tỏ như sau:
1. Sử dụng khái niệm lối trung bình:
- Đường tầm của tam giác là đoạn trực tiếp nối một đỉnh của tam giác với trung điểm của cạnh đối lập đỉnh cơ.
- Cạnh loại tía là cạnh không khí bịa đặt không giống với cạnh đối lập đỉnh đang được xét.
2. Sử dụng đặc thù tuy vậy song:
- Hai đường thẳng liền mạch sẽ là tuy vậy song nếu như bọn chúng ko tách nhau, tức không tồn tại điểm công cộng này.
- Đường tầm của tam giác được xác lập vì thế thành quả của tia trải qua trung điểm của cạnh đối lập.
- Vì lối tầm và cạnh loại tía đều trải qua trùng điểm cạnh đối lập, nên bọn chúng ko tách nhau, bởi vậy, bọn chúng là tuy vậy song cùng nhau.
3. Chứng minh vì thế hình học:
- Vẽ một tam giác ABC với lối tầm AD của cạnh BC.
- Cân tam giác ABC bên trên A nhằm AM là lối cao của tam giác.
- Khi cơ, AM tiếp tục tách BC bên trên trung điểm M của cạnh BC.
- Vẽ đường thẳng liền mạch EF tuy vậy song với AB, tách AM bên trên E và tách AC bên trên F.
- Ta cần thiết chứng tỏ rằng EM và AF là tuy vậy tuy vậy.
- Với TAM và TAC là những tam giác đồng dạng (vì AM tuy vậy song với BC), tớ sở hữu tỷ số đồng dạng như sau:
- AE/AB = AM/AC và AF/AC = AM/AB
- Từ cơ, tớ có: AE/AF = AB/AC
- Do nhị cạnh mặt mày của TAM và TAC tuy vậy song cùng nhau, tỷ số đều nhau, rút gọn gàng tớ được: AE/AF = AB/AC = EM/AF (do EM = AB và AF = AC)
- Từ cơ suy đi ra EM = AF
- Vậy lối tầm EM tuy vậy song với cạnh loại tía AF.
Tóm lại, tớ đang được thấy rằng lối tầm của tam giác hoàn toàn có thể được xác lập là tuy vậy song với cạnh loại tía trải qua những cách thức chứng tỏ và đặc thù hình học tập của tam giác.
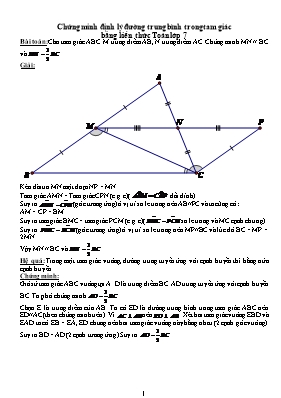
Đường tầm tam giác, hình thang (Phần 1) - Bài 4 - Toán 8 - Cô Huệ Chi (DỄ HIỂU NHẤT)
Hãy coi đoạn Clip này nhằm tò mò về lối tầm tam giác, một định nghĩa cần thiết vô hình học tập. quý khách hàng sẽ tiến hành chỉ dẫn phương pháp tính toán lối tầm tam giác và vận dụng nó vô giải những bài xích tập luyện thú vị.
Làm thế này nhằm chứng tỏ rằng một quãng trực tiếp là lối tầm của tam giác?
Để chứng tỏ rằng một quãng trực tiếp là lối tầm của tam giác, tất cả chúng ta hoàn toàn có thể vận dụng một trong mỗi cách thức sau:
1. Sử dụng đặc thù lối trung bình: Để chứng tỏ rằng đoạn trực tiếp AB là lối tầm của tam giác ABC, tớ cần thiết chứng tỏ rằng AB tuy vậy song với cạnh loại tía và có tính lâu năm vì thế 1/2 cạnh cơ.
- Để chứng tỏ AB tuy vậy song với cạnh loại tía, tớ hoàn toàn có thể dùng tính chất tuy vậy song của những đường thẳng liền mạch.
- Để chứng tỏ chừng lâu năm AB vì thế 1/2 cạnh loại tía, tớ cần thiết đối chiếu chừng lâu năm AB với chừng lâu năm cạnh loại tía và chứng tỏ rằng bọn chúng đều nhau.
2. Sử dụng đặc thù điểm trung điểm: Để chứng tỏ rằng đoạn trực tiếp AB là lối tầm của tam giác ABC, tớ cần thiết chứng tỏ rằng A là trung điểm của BC.
- Để chứng tỏ A là trung điểm của BC, tớ hoàn toàn có thể dùng đặc thù trung điểm nhưng mà tớ đang được biết.
- Nếu tớ hoàn toàn có thể chứng tỏ A là trung điểm của BC, thì tớ đã và đang chứng tỏ rằng AB là lối tầm, vì thế đường thẳng liền mạch nối trung điểm của một cạnh với đỉnh đối lập vô tam giác là lối tầm của tam giác.
3. Sử dụng đặc thù tương tự: Để chứng tỏ rằng đoạn trực tiếp AB là lối tầm của tam giác ABC, tớ cần thiết chứng tỏ rằng đoạn trực tiếp AB tương tự động đoạn trực tiếp AC và AB bao gồm 1/2 số đo của AC.
- Để chứng tỏ điều này, tớ cần thiết đối chiếu số đo của AB và số đo của AC và chứng tỏ rằng bọn chúng sở hữu quan hệ tương tự động.
Tùy vô những vấn đề rõ ràng nhưng mà tớ sở hữu về tam giác và đoạn trực tiếp, tất cả chúng ta hoàn toàn có thể vận dụng những cách thức bên trên nhằm chứng tỏ rằng một quãng trực tiếp là lối tầm của tam giác.
Đường tầm của tam giác sở hữu Điểm lưu ý gì?
Đường tầm của tam giác sở hữu những Điểm lưu ý sau:
1. Đường tầm của tam giác là đoạn trực tiếp nối trung điểm của nhị cạnh tam giác với đỉnh của cạnh sót lại.
2. Đường tầm của tam giác là đường thẳng liền mạch trải qua trung điểm của tam giác.
3. Đường tầm của tam giác sở hữu tầm quan trọng phân chia song diện tích S của tam giác.
4. Đường tầm của tam giác tuy vậy song với 1 cạnh của tam giác và vì thế 1/2 cạnh cơ.
5. Đường tầm của tam giác là 1 trong những trong mỗi lối trung tuyến vô tam giác.
6. Trong một tam giác cân nặng, lối tầm của tam giác là khớp với lối cao và lối trung trực kể từ đỉnh của tam giác.
Hy vọng những vấn đề bên trên tiếp tục khiến cho bạn nắm rõ về lối tầm của tam giác.

Xem thêm: acrylic an cường
_HOOK_
ĐỊNH NGHĨA, ĐỊNH LÍ, TÍNH CHẤT ĐƯỜNG TRUNG BÌNH TAM GIÁC. TOÁN LỚP 8-P1
Bạn vẫn muốn biết đặc thù quan trọng của lối tầm tam giác? Video này tiếp tục hỗ trợ cho chính mình vấn đề quan trọng về tính chất đối xứng, tính quan trọng của những lối tầm và quy tắc cần thiết Lúc chứng tỏ đặc thù này.
Tại sao lối tầm của tam giác vì thế nửa cạnh ấy?
Đường tầm của tam giác vì thế nửa cạnh ấy được chứng tỏ vì thế công việc sau:
Bước 1: Kẻ lối cao kể từ đỉnh của tam giác xuống đối lập với cạnh cơ. Vấn đề này tạo ra trở nên nhị tam giác vuông sở hữu cạnh lòng công cộng.
Bước 2: Xem xét tam giác vuông nhưng mà lối cao trực thuộc cơ. Gọi cạnh lòng của tam giác vuông là a, và lối cao của chính nó là h.
Bước 3: Đặt A là đỉnh của tam giác, B và C theo lần lượt là những đỉnh bên trên cạnh lòng của tam giác vuông cơ.
Bước 4: Do tam giác ABC là tam giác vuông, tớ sở hữu nhị tỉ số sau:
a/h = h/a
Bước 5: Giải phương trình tỉ số:
a^2 = h^2
Bước 6: kề dụng lăm le lý Pythagoras vô tam giác vuông ABC, tớ có:
a^2 = b^2 + c^2
Bước 7: Do lối cao h vô tam giác ABC tạo ra trở nên nhị tam giác vuông sở hữu cạnh lòng công cộng, tớ có:
b = h và c = a - h
Bước 8: Thay b và c vô phương trình Pythagoras, tớ có:
a^2 = h^2 + (a - h)^2
Bước 9: Mở ngoặc ở bên phải của phương trình, tớ có:
a^2 = h^2 + a^2 - 2ah + h^2
Bước 10: Thu gọn gàng phương trình, tớ có:
0 = 2h^2 - 2ah
Bước 11: Chia từng member của phương trình cho tới 2h, tớ có:
0 = h - a/2
Bước 12: Do lối cao và cạnh lòng của tam giác đồng dạng, tớ có:
h/a = a/2h
Bước 13: Đổi địa điểm thay đổi vô phương trình bên trên, tớ có:
a/h = 2h/a
Bước 14: Từ công việc bên trên, tớ thấy rằng a/h = h/a = 2h/a.
Vậy, lối tầm của tam giác vì thế nửa cạnh ấy.
Làm thế này nhằm chứng tỏ lối tầm vô tam giác cân?
Để chứng tỏ lối tầm của tam giác cân nặng, tớ cần thiết tuân theo công việc sau đây:
Bước 1: Cho tam giác ABC cân nặng bên trên A.
Bước 2: Gọi M là trung điểm của cạnh BC.
Bước 3: Vẽ lối tầm AM của tam giác ABC.
Bước 4: Ta cần thiết chứng tỏ rằng lối tầm AM // cạnh AB và AM có tính lâu năm vì thế 1/2 cạnh AB.
Bước 5: kề dụng khái niệm lối tầm vô tam giác, tớ có:
AM là lối tầm của tam giác ABC ⇔ AM // cạnh AB và AM có tính lâu năm vì thế 1/2 cạnh AB.
Bước 6: Để chứng tỏ điều bên trên, tớ dùng công thức trung điểm và những lăm le lý về tam giác, như sau:
- Vì M là trung điểm của cạnh BC, nên BM = MC.
- Vì tam giác ABC là tam giác cân nặng bên trên A, nên lối cao kể từ A xuống BC tách BC bên trên trung điểm M.
- kề dụng lăm le lý về tam giác cân nặng, tớ sở hữu AM // cạnh AB và AM có tính lâu năm vì thế 1/2 cạnh AB.
Bước 7: Do AM // cạnh AB và AM = 50% AB, nên tớ đang được chứng tỏ AM là lối tầm của tam giác ABC.
Lưu ý: Trong quy trình chứng tỏ, hoàn toàn có thể dùng những lăm le lý và khái niệm tương quan cho tới tam giác, tổng thể hoặc toàn viên, nhằm thực hiện rõ ràng những quy tắc và bước chứng tỏ.
Trường phù hợp này vô tam giác không tồn tại lối trung bình?
Trường phù hợp vô tam giác không tồn tại lối tầm là lúc tam giác cơ không tồn tại một đường thẳng liền mạch này phân chia một cạnh trở nên nhị phần đều nhau. Vấn đề này hoàn toàn có thể xẩy ra vô một vài tình huống sau:
1. Tam giác cân: Trong tam giác cân nặng, lối tầm được xác lập vì thế lối tròn trặn nước ngoài tiếp tam giác. Do cơ, vô tam giác cân nặng, luôn luôn tồn bên trên tối thiểu một lối tầm.
2. Tam giác đều: Trong tam giác đều, những cạnh và góc của tam giác đều đều nhau. Trong tam giác đều, lối tầm là những đường thẳng liền mạch tách nhau bên trên trọng tâm tam giác. Do cơ, vô tam giác đều, luôn luôn tồn bên trên lối tầm.
3. Tam giác vuông: Trong tam giác vuông, lối tầm của tam giác là đoạn trực tiếp nối trung điểm của cạnh góc vuông và đỉnh ko nằm trong cạnh góc vuông. Do cơ, vô tam giác vuông, luôn luôn tồn bên trên lối tầm.
Tuy nhiên, trong những tam giác ko với những tình huống bên trên, như tam giác không đồng đều và ko cân nặng, hoàn toàn có thể ko tồn bên trên lối tầm. Trong tình huống này, lối tầm ko thể vẽ vì thế một quãng trực tiếp ở trọn vẹn vô tam giác và phân chia cạnh trở nên nhị phần đều nhau.
Cách chứng tỏ lối tầm tam giác | Math CASIO
Nếu các bạn đang được thăm dò hiểu cơ hội chứng tỏ đặc thù lối tầm tam giác, hãy coi đoạn Clip này. quý khách hàng sẽ tiến hành chỉ dẫn qua chuyện từng bước cơ hội chứng tỏ và có được những khêu gợi ý cần thiết nhằm thành công xuất sắc trong các công việc chứng tỏ đặc thù này.
Đường tầm của tam giác sở hữu phần mềm gì vô thực tế?
Đường tầm của tam giác có tương đối nhiều phần mềm vô thực tiễn như sau:
1. Xác xác định trí trọng tâm: Đường tầm của tam giác tách nhau bên trên một điểm gọi là trọng tâm. Trọng tâm là vấn đề kí thác của tía lối tầm, phía trên một lối quý phái tâm. Trọng tâm được dùng vô tiến độ tham khảo, kiến thiết và kiến tạo những dự án công trình nhằm đáp ứng bằng phẳng và ổn định lăm le.
2. Xác lăm le điểm tâm của lối tròn trặn nước ngoài tiếp: Đường tầm của tam giác bên cạnh đó là lối cao và lối trung trực nên lúc kẻ lối tầm của tam giác và nối những đỉnh với trung điểm ứng, tớ hoàn toàn có thể xác lập điểm tâm của lối tròn trặn nước ngoài tiếp.
3. Phân tích và thăm dò hiểu những đặc thù của tam giác: Đường tầm của tam giác hoàn toàn có thể hùn tất cả chúng ta phân tách và thăm dò hiểu những đặc thù cơ phiên bản của tam giác như lối cao, lối trung trực và trực tâm..
4. Xác lăm le đặc điểm về hình học: Đường tầm của tam giác cũng cho tới tất cả chúng ta biết về đặc điểm hình học tập của tam giác như đặc thù của những lối tuy vậy song và tỷ trọng Một trong những cạnh và lối tầm.
5. Ứng dụng vô giám sát và tỷ lệ: Đường tầm của một tam giác cũng hoàn toàn có thể được dùng nhằm đo lường và xác lập tỷ trọng Một trong những cạnh và những đoạn trực tiếp vô tam giác.
Đường tầm của tam giác có tương đối nhiều phần mềm và góp sức cần thiết trong nghề hình học tập và thực tiễn. Việc hiểu và vận dụng lối tầm của tam giác không chỉ là tăng thêm ý nghĩa vô dạy dỗ nhưng mà còn khiến cho tất cả chúng ta cải cách và phát triển năng lực suy nghĩ và áp dụng những định nghĩa hình học tập vô những yếu tố thực tiễn.
Xem thêm: quy đổi inch sang cm
Làm thế này nhằm xác lập những điểm bên trên lối tầm của tam giác?
Để xác lập những điểm bên trên lối tầm của tam giác, tất cả chúng ta hoàn toàn có thể vận dụng những cách thức sau đây:
1. Sử dụng công thức nhằm tính tọa chừng của điểm trung điểm:
- Với tam giác ABC, Một cơ hội dễ dàng và đơn giản nhằm xác lập điểm trung điểm của một cạnh là lấy tầm của nhị tọa chừng của những điểm cuối của cạnh cơ. Ví dụ: Trong tam giác ABC với nhị đỉnh là A(0,0) và B(4,6), tớ hoàn toàn có thể tính tọa chừng của trung điểm của cạnh AB bằng phương pháp lấy tầm của tọa chừng của A và B: (0+4)/2 và (0+6)/2, tớ sẽ sở hữu trung điểm của AB là (2,3).
2. kề dụng đặc thù lối trung bình:
- Đường tầm của tam giác là đoạn trực tiếp nối một điểm vô tam giác với trung điểm của cạnh ứng. Ví dụ, nhằm xác lập lối tầm của đoạn trực tiếp AB vô tam giác ABC, tớ cần thiết thăm dò trung điểm của AB và liên kết nó với 1 điểm ngẫu nhiên vô tam giác ABC (trừ A và B). Kết trái ngược là đường thẳng liền mạch nối điểm trung điểm và điểm được lựa chọn bên trên tam giác.
3. Sử dụng đặc thù tuy vậy song:
- Một đặc thù cần thiết của lối tầm là nó tuy vậy song với cạnh ứng của tam giác. Vấn đề này Tức là lối tầm của một cạnh sẽ không còn tách cạnh không giống. Ví dụ: Trong tam giác ABC, nếu như tớ biết lối tầm của cạnh AB tuy vậy song với cạnh AC, tớ hoàn toàn có thể dễ dàng và đơn giản thăm dò điểm bên trên lối tầm của cạnh AB bằng phương pháp dựng một đường thẳng liền mạch tuy vậy song với cạnh AC và thăm dò nút giao của đường thẳng liền mạch cơ với cạnh AB.
Một điểm cần thiết nhằm xác lập những điểm bên trên lối tầm của tam giác là hiểu và vận dụng những đặc thù và lăm le lý tương quan cho tới tam giác và đường thẳng liền mạch vô không khí hai phía.
_HOOK_











Bình luận